Si llegaste a este blog, probablemente ya hayas escuchado términos como ser “data analytics”, “machine learning” o bien “data science”. Si bien estos tópicos están muy de moda, no debemos olvidar que todos ellos están íntimamente relacionados con la estadística descriptiva.
Por eso dedicaremos este artículo a entender algunos conceptos muy importantes de la rama estadística que te permitirán ser un mejor analista de datos.
A menudo trabajamos con muchísimos datos, es por eso que recurrimos a dos tipos de medidas estadísticas que nos permiten entender mejor la distribución de la muestra o población en estudio, estas son las medidas de tendencia central u las medidas de dispersión.
Medidas de tendencia central
Las medidas de tendencia central son parámetros estadísticos que intentan representar en un numero al conjunto de valores en estudio. Este parámetro se ubica hacia el centro de la distribución.
Las medidas de tendencia central nos sirven para poder comparar datos, muestras o poblaciones entre sí. También nos ayudan a interpretar datos que puedan resultar erróneos, improbables, anómalos que estén fuera del rango posible de ocurrencia.
Cuando hablamos de medidas de tendencia central, podemos mencionar las siguientes:
Media:
Es la medida de tendencia central más utilizada y conocida. Se la suele llamar promedio, aunque debemos decir que debido a que existen varios tipos de promedio el término correcto sería promedio aritmético. La media o promedio aritmético se obtiene sumando todos los números de la muestra o población para luego dividirlo por la cantidad de los elementos en estudio.
Mediana
La mediana se define como el valor que ocupa exactamente la mitad de los datos, es decir que, si pudiéremos ordenar el conjunto de datos de mayor a menor, la mediana se ubicaría en un valor que sería mayor a la mitad de los valores de la serie y a su ves también sería menor al resto de los valores.
Aprovechamos para mencionar que tanto la media como la mediana, pueden resultar en valores que no pertenezcan al conjunto de datos evaluados.
Moda
Es el valor que aparece con mayor frecuencia en el conjunto de datos, o dicho de otra manera el que más se repite.
Es conveniente mencionar que las medidas de tendencia central no dicen nada por si solas, y es conveniente siempre estudiarlas en conjunto con las llamadas medidas de dispersión.
Medidas de dispersión
Las medidas de dispersión son estadísticos que nos dan información al respecto de la variabilidad o separación de los datos generalmente respecto a la media. Nos ayudan a comprender la distribución de los datos y evitan tomar conclusiones erróneas al comparar distintos grupos.
Hay muchos estadísticos de dispersión, no obstante mencionaremos los más utilizados.
Rango
Es el más fácil de calcular y se define como la distancia que hay entre el valor mas grande y el valor mas chico de la muestra. Nos permite tener una idea inicial de la variabilidad de los datos.
Varianza
Se calcula como el promedio del cuadrado de las desviaciones de cada dato del conjunto respecto a su media. Es conveniente mencionar que en este caso la potencia permite trabajar todos los desvíos como positivos independientemente de que la diferencia de cada dato sea negativa.
Desvió estándar
También conocida como el desvío típico. Se calcula como la raíz cuadrada de la varianza. Al igual que la varianza antes descripta representa variabilidad de los datos, pero mantiene las unidades de la variable evaluada.
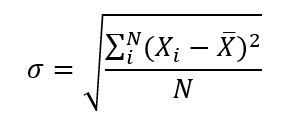
Cuartiles
Los cuartiles son términos estadísticos que describen los datos en 4 grupos. Para entender los cuartiles debemos recordar la previamente citada mediana. La mediana era un valor que dejaba la mitad de los datos a cada lado. Los cuartiles vuelven a dividir estos dos subgrupos en nuevas mitades, es decir, cuartos. El primer cuartil (generalmente llamado Q1) contiene el 25% de los datos más pequeños, a su vez, el cuartil 3 (Q3) es un valor que se sitúa justo en la mitad entre la mediana y el valor más alto de la distribución. Los cuartiles nos permiten entender cómo se distribuyen los valores alrededor de la mediana, y nos brindan mucha información adicional sobre la variable en estudio.
Podríamos seguir citando estadísticos adicionales, pero ahora creemos conveniente definir un nuevo grupo de medidas de dispersión, las llamadas dispersiones relativas.
Medidas de dispersión relativa
Estos estadísticos nos permiten comparar distintas poblaciones y sus distribuciones. Los más usados son:
Coeficiente de variación
Se define como la relación entre la media y el desvío estándar. Nos permite evaluar que tan dispersos están los datos respecto a la media.
CV = σ / Media
Coeficiente de rango
Se calcula como la relación entre el rango respecto de la suma de los valores máximo más el valor mínimo.
(Valor Máximo – valor Mínimo) / (Valor Máximo + Valor Mínimo)
Coeficiente de la desviación de los cuartiles:
Es muy similar al punto anterior, pero en este caso, se compara la distancia entre el Q3 y el Q1, respecto del la suma de ambos.
(Q3 – Q3) / (Q3 + 1)
¿Cuánta información no?
Como verás el camino a convertirse en un gran analista de datos e involucrarse en la gestión data driven es toda una aventura infinita y ya estás un poquito más cerca.
¿Querés iniciarte en el mundo de los datos? Te interesa el data science, machine learning y data analytics? Si la respuesta es afirmativa, podes pegarte una vuelta por nuestro sitio donde encontrarás todo lo necesario para que se vuelva realidad.
Si queres conocer cómo aplicar la estadística descriptiva a casos de negocio podes contactarte con los especialistas en datos de Maseldata😉. ¡Te esperamos en la siguiente nota!